<MOS> 3. Operation modes 수식 유도

"<MOS> 1. MOS 구조의 정성적 해석"에서 MOS capacitor에 인가한 $V_G$(gate voltage)에 따라, 3가지 operation mode(accumulation, depletion, inversion mode)를 정의했다. 이번 챕터에서는 직전 챕터에서 유도한 parameter들을 활용하여 operation mode들을 수식으로 유도해볼 것이다.
$ $
아래의 두 개의 parameter 활용하여 수식을 유도할 것이니, 아래의 관계식이 잘 기억이 나지 않는다면 이전 챕터를 꼭 공부하고 오기를 바란다.

① $V_G < 0 < V_{FB}$일 때: Accumulation mode

(참고: Semiconductor Physics&nbsp;and Devices&nbsp;(Donald A. Neamen))

위는 accumulation mode의 MOS capacitor로, 이전에 배웠다시피 (+) charge의 hole들이 Si surface로 몰려 축적되는 operation mode이다. 이때, metal에 인가된 전압에 의한 $Q_m$에 대응되는 $Q_s$가 생성된다. 이때, accumalation mode에서의 $Q_s$를 $Q_{acc}$라고 한다.

하지만, 이전 챕터에서 배웠듯이 accumulation mode에서 $\phi_s$는 거의 변하지 않는다. 왜냐하면 $\rho_s$는 $\phi_s$가 조금만 변하더라도 매우 크게 변하기 때문이다. 따라서 $\phi_s \approx 0$이다(Gate에 인가된 전압 중 아주 적은 양의 voltage만 semiconductor에 영향을 줘서 $\phi_s \approx 0$이라고 생각해도 된다). 이는 아래의 수식으로도 확인할 수 있다. 아래의 $\rho_s$ 수식을 보면 exp함수에 의해 $\phi_s$가 조금만 변해도 $\rho_s$가 매우 크게 변한다는 것을 알 수 있다.

$\phi_s$와 $\rho_s$ 관계식

이와같은 특징($\rho_s$ = 0)을 고려하여 아래와 같이 수식을 전개해보자.

위 수식을 통해, $Q_{acc} = Q_s$는 $v_G$에 비례한다는 사실을 알 수 있다.

② $V_G = V_{FB}$일 때: Flat Band Voltage

(참고: Semiconductor Physics&nbsp;and Devices&nbsp;(Donald A. Neamen))

위의 그림은 MOS Capacitor에 $V_{FB}$를 인가했을 때의 이상적인 energy band diagram이다.
$V_{FB}$를 인가하면 band bending이 사라지고 semiconductor에서의 fermi-level이 일정하게 유지된다. Band bending이 사라지므로 $\phi_s(surface potential) = 0, V_{ox} = 0, Q_s = 0$이 된다. 이를 정리하면 아래와 같은 수식을 얻을 수 있다. 즉, $V_{FB}$는 접합 전의 $E_{FM}$과 $E_{FS}$만큼의 차이이다.

그런데 이때 모순점을 찾을 수 있다. Metal에 $V_{FB}$의 전압이 인가되면 metal과 oxide의 접합면에 $Q_m$만큼의 charge가 발생할 것이다. 그렇다면 그에 대응하는 image charge인 $Q_s$가 발생해야하는데, 앞서 언급했듯이 $Q_s = 0$이다. 이와 같은 모순은 oxide에 의해 해결된다. oxide에는 charge가 없는 절연체라고 다들 알고있지만, 사실 oxide 표면에 어느정도의 charge($Q_i$)가 존재한다. 따라서, $Q_i$가 image charge가 되어 $Q_m$에 대응되어 균형을 맞춘다. 아래의 그림을 보면 이해가 될 것이다. (따라서 flat band voltage는 $Q_i$까지 고려한 전압이다)

③ $V_{FB} < V_G < V_T$일 때: Depletion mode

(참고: Semiconductor Physics&nbsp;and Devices&nbsp;(Donald A. Neamen))

위의 그림은 depletion mode의 MOS capacitor로 metal에 인가된 (+) charge에 의해 semiconductor의 hole들이 경계면에서 멀어져 depletion region이 형성된 상태이다. Depletion region에 의한 charge $Q_s$ $-qN_Ax_d$이고 이것을 $Q_{dep}$라고 한다. 마찬가지로 $Q_{dep}$는 $Q_m$에 대응되는 charge이다.

이제 depletion mode를 아래와 같이 수식으로 전개해보자.

위의 최종 수식을 통해, $Q_{dep}(=Q_s)$는 $\sqrt{V_G}$에 비례한다는 것을 알 수 있다. 추가적으로 $Q_{dep} = -qN_Ax_d$와 $x_d = \sqrt{\frac{2\epsilon_s\phi_s}{qN_A}}$를 통해 $Q_{dep}(=Q_s)$가 $\sqrt{\epsilon_s}$에도 비례한다는 것을 알 수 있다.

④ $V_G = V_T$일 때: Threshold Voltage

(참고: Semiconductor Physics&nbsp;and Devices&nbsp;(Donald A. Neamen))

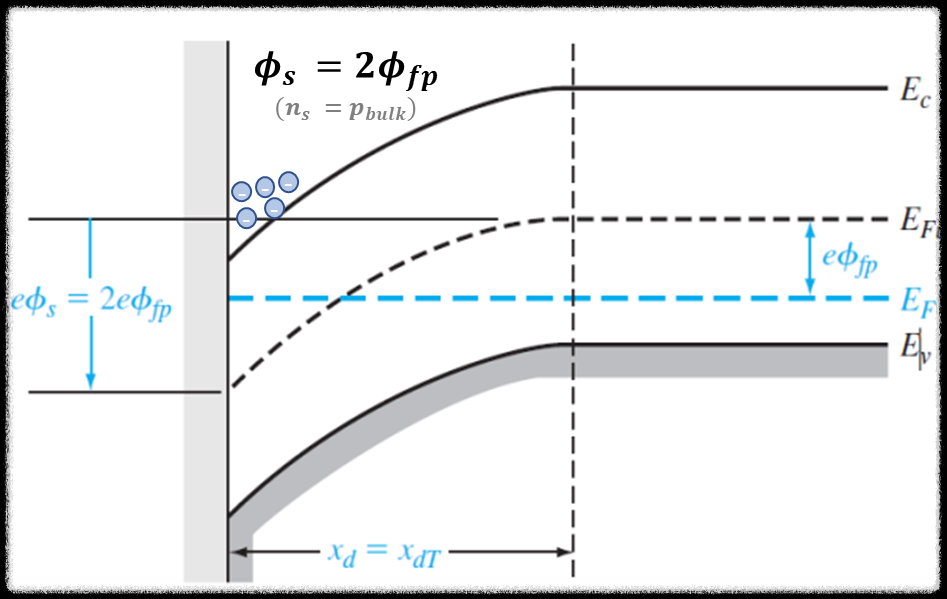
위의 그림은 threshold voltage $V_T$를 인가했을 때의 energy band diagram이다. 위의 그림을 자세히 보면 경계면에 minority carrier인 전자가 모여있는 것을 볼 수 있다. 이는 metal에 인가된 강한 전압에 의해 minority carrier가 경계면으로 몰려드는 것이다. Band diagram의 fermi-level을 보아도 알 수 있듯이, fermi-level이 p-type semiconductor임에도 불구하고 경계면에서는 n-type과 같이 conduction band에 더 가까운 것을 확인할 수 있다. 다시말해, threshold voltage가 인가된 상황에서는 이미 형성된 depletion region에 의한 charge에 추가적으로 전자에 의한 inversion charge가 형성된다. 수식으로 정리하자면, $Q_m$에 대응되는 $Q_s = Q_{dep} + Q_{inv}$이다. 이때, $\phi_s = 2\phi_{fp}$...즉, $n_s = p_{bulk}$이므로 $Q_{dep}$와 $Q_{inv}$는 모두 $-qN_A$로 같다. 이해가 잘되지 않는다면 아래의 그림을 글과 함께 비교하면 살펴보기를 바란다.

이제 threshold voltage를 인가했을 때를 수식으로 표현해보자. $V_T$를 인가하면 $\phi_s = 2\phi_{fp}$이므로 $\phi_s$는 $2\phi_{fp}$로 바꾸어 표현해도록 하겠다.

⑤ $V_G > V_T$일 때: (Strong) Inversion mode

(참고: Semiconductor Physics&nbsp;and Devices&nbsp;(Donald A. Neamen))

위는 MOS capacitor의 동작 모드 중 하나인 inversion mode로, $V_T$보다도 큰 전압을 인가했을 때의 동작 모드이다. 이때 인가된 전압은 threshold voltage 이상의 전압이므로 앞선 챕터에서 배웠듯이 $\phi_s \approx 2\phi_{fp}$이고 마찬가지로 depletion width인 $x_d \approx x_{dT} = \sqrt{\frac{2\epsilon_s(2\phi_{fp})}{qN_A}}$임을 알 수 있다. 이와 같은 상태에서 굉장히 강한 전압이 인가되었기에 minority carrier가 위의 그림처럼 경계면 쪽으로 더욱 모여드는 것을 확인할 수 있다. 당연히 minority carrier에 의한 charge는 급격하게 증가한다. 수식으로 표현하면 $Q_s = Q_{dep}(고정) + Q_{inv}(증가)$이다. 아래 그림을 참고하면 이해가 될 것이다.

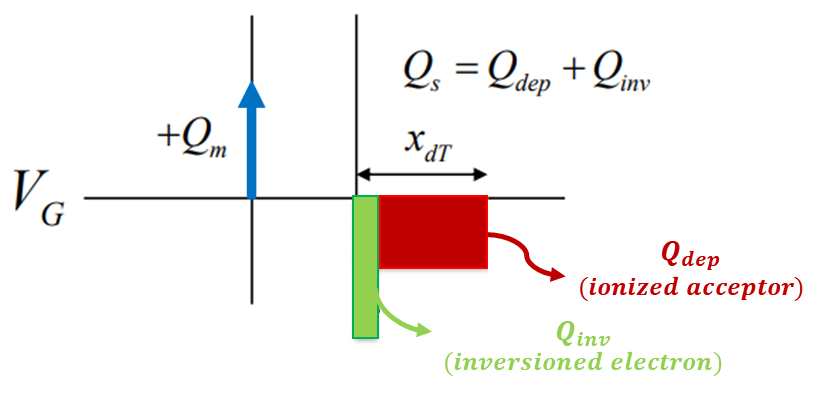
이제 Inversion mode를 수식으로 표현해보면, $Q_{acc} = -C_{ox}(V_G - V-{FB})$와 유사한 것을 알 수 있다.

$V_G$에 따른 $\phi_s$와 $x_d$, $Q_s$

위에서 도출한 수식을 통해 $V_G$에 따른 $\phi_s$와 $x_d$를 그래프로 표현하면 아래와 같이 정리할 수 있다.

(참고: Semiconductor Physics&nbsp;and Devices&nbsp;(Donald A. Neamen))

(참고: Semiconductor Physics&nbsp;and Devices&nbsp;(Donald A. Neamen))

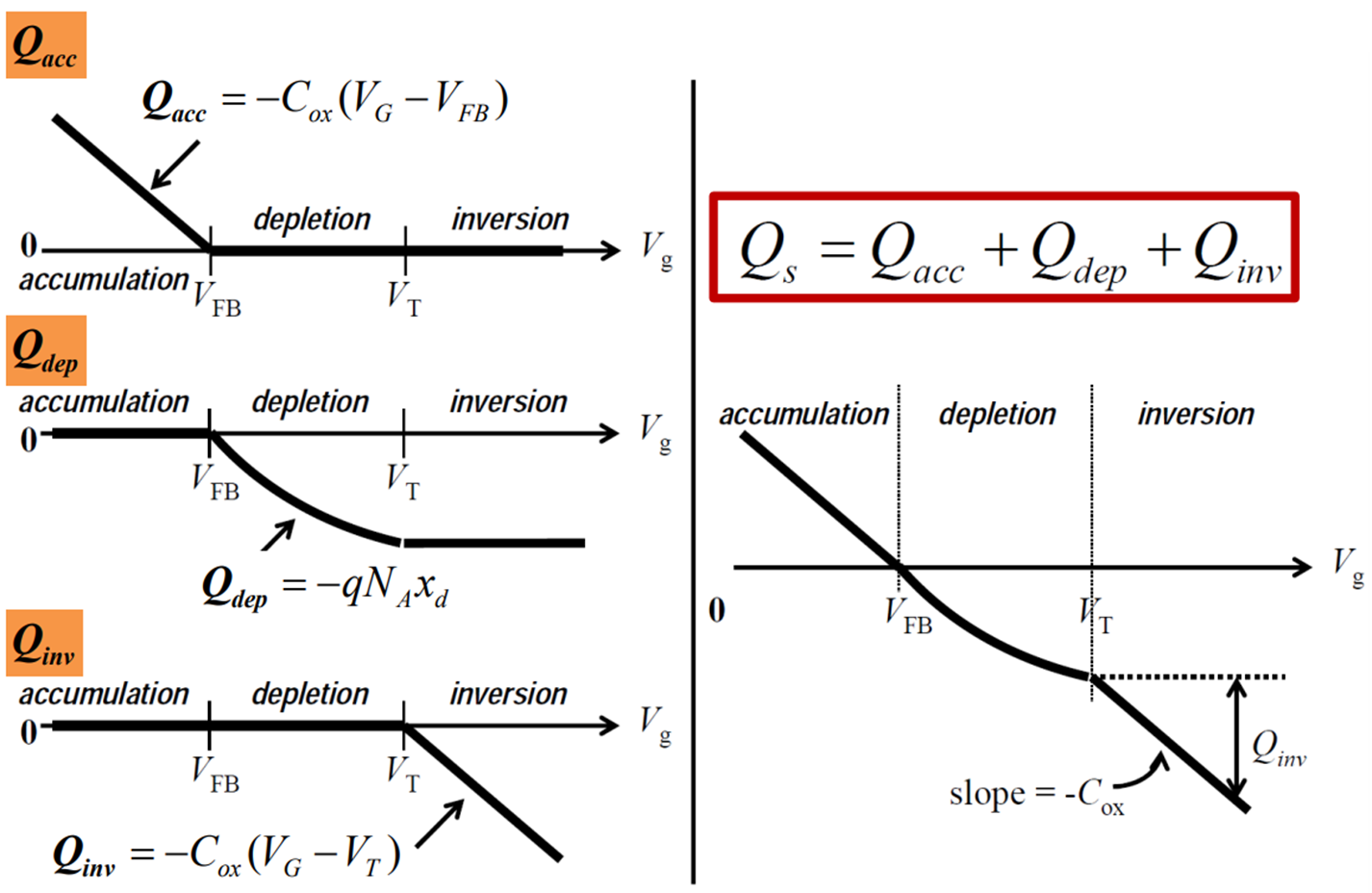
마찬가지로 도출한 charge 수식을 통해, total charge density $Q_s = Q_{acc} + Q_{dep} + Q_{inv}$를 아래와 같이 그릴 수 있다. 아래의 그래프는 MOS capacitor뿐만 아니라 MOSFET을 이해할 때도 굉장히 중요한 역할을 하기 때문에 위의 operation mode 수식 유도 과정부터 아래 그래프까지 완벽히 이해하기를 바란다.

(참고: https://youtube.com/playlist?list=PLcfIhRUEj9uAVHkFy5rbY-0pzWcZlU-0h)

 

 

---

작성자: 이현우 / 수정 및 검토: 손동휘, 김현수