<MOS> 1. MOS 구조의 정성적 해석

반도체에 관심이 있는 사람이라면 MOS라는 단어를 어디선가 한 번은 들어보았을 것이다. 그렇다. 바로 MOSFET에서의 MOS이다. 간단히 설명하자면, MOS는 Metal Oxide Semiconductor의 준말로 반도체를 다룰 때 가장 중요한 소자인 MOSFET의 구조가 MOS이다. 이번 시간에는 이후에 배우게 될 MOSFET을 이해하기에 앞서 MOS 구조에 대한 정성적인 해석과 Energy band diagram을 그려보고 전압을 인가했을 때의 특징에 대해 알아볼 것이다.

MOS구조와 MOSFET

Structure

(참고: Semiconductor Physics and Devices (Donald A. Neamen), Sungho Kim youtube)

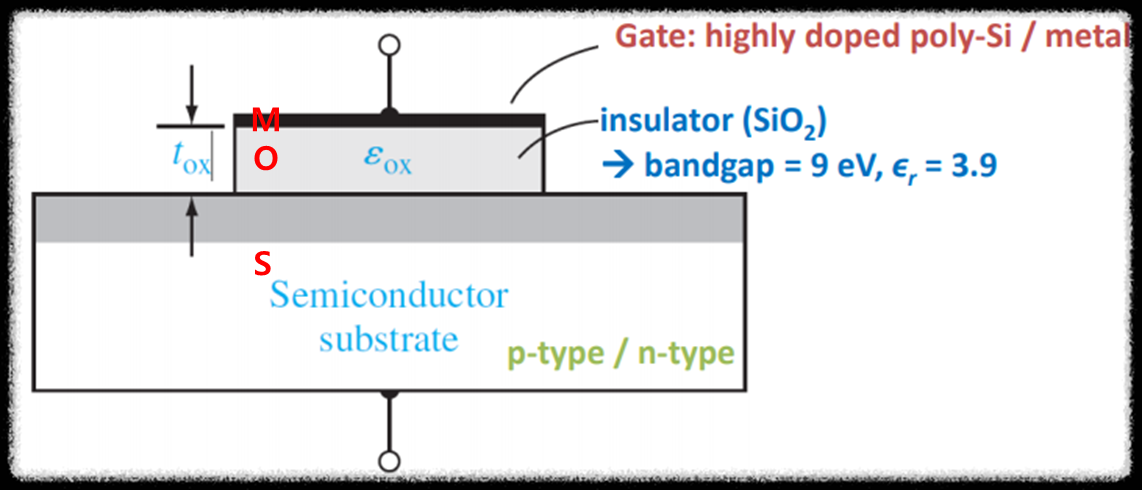
위의 구조는 MOS Capacitor의 구조이다. MOS capacitor의 구조는 앞서 이야기했듯이, metal + oxide + semiconductor의 구조이다.
$ $
우선, metal부터 살펴보자. MOS 구조에서 metal은 주로 gate라고 부른다. 당연히 gate를 이루는 재료는 metal이다. 참고로 highly doped poly-Si를 gate의 재료로서 사용하기도 하는데, 이는 도핑 농도가 매우 높아 metal과 같은 역할을 할 수 있기 때문이다(poly-Si인 이유는 single-crystal Si wafer와 다르게, 증착 과정을 거쳐 만들어야하므로 poly-crystal 구조를 갖기 때문이다). 그리고 위의 그림에서도 알 수 있듯이, gate에는 전극과 연결되어 있는데, 여기서 인가되는 전압을 $V_G$라고 한다.
$ $
다음으로 gate 아래의 oxide를 살펴보자. 여기서 oxide(산화물)는 밴드갭 에너지가 매우 큰 절연체 역할을 하는데, 주로 절연 특성이 우수하고 절연체 생성에 용이한 $SiO_2$를 사용한다(생성이 용이한 이유는 아래 기판인 Si를 산화시키면 $SiO_2$가 되기 때문이다). Oxide의 가장 중요한 요소는 $t_{ox}$(두께)와 $\epsilon_{ox}$(유전율)이다. 이에 대한 자세한 설명은 추후에 다루도록 하겠다.
$ $
마지막으로 semiconductor substrate(기판)을 살펴보도록 하겠다. Gate에서 잠깐 언급했듯이, semiconductor substrate는 single-crystal Si wafer로 accpetor를 인가한 p-type 혹은 donor를 인가한 n-type semiconductor를 사용한다. Gate에서와 마찬가지로 semiconductor substrate에도 전극이 연결되어있다. 이곳에서 인가되는 전압을 $V_{sub}$라고 하는데, 일반적인 경우 전압을 인가하는 전극이 아닌 접지로 활용된다.

Energy Band Diagram

(참고: Semiconductor Physics and Devices (Donald A. Neamen))

위의 그림은 metal, oxide, p-type silicon semiconductor 각각의 energy band diagram이다. 이제 이들 모두를 접합한 MOS의 energy band diagram을 그려보도록 하자.
$ $
Energy band diagram을 그릴 때의 핵심은 fermi-level을 일치시키는 것이다. 어떤 물질이든 접합이 이루어진 후 thermal-equilibruim이 되면 fermi-energy는 동일하다. 그렇기 때문에 우리는 fermi-level($E_F$)를 일치시키는 것을 최우선으로 하고 energy band diagram을 그려야한다. Fermi-level을 MOS 전체에 걸쳐 일정하게 그렸다면, 항상 일정한 고유값들을 고려하여 energy band diagram을 그리면 된다. 글로만 봐서는 이해가 되지 않을 것이니 아래 그림을 살펴보자.

(참고: Semiconductor Physics and Devices (Donald A. Neamen))

위와 같이 우리가 알고있는 고유값인 $\phi_m$, $\chi_i$, $\chi$, $E_g$ 등을 활용하여 고정점을 그린 후 $E_F$를 일치시키면 된다. 이때 band diagram을 그리기 위해 고려해야할 추가적인 3가지 특징에 대해 간단히 알아보자.
$ $

• 먼저 semiconductor 영역에서는 $E_F$는 수평하다. oxide 영역에 막혀 전류가 흐를 수 없기 때문이다(carrier가 이동하지 않는다). 따라서 semiconductor 영역에서는 $E_F$를 수평하게 그려줘야한다.
• 다음으로, oxide 영역에서 band bending이 선형적이다. 절연체인 oxide는 $\rho = 0$, $\frac{dE}{dx} = 0$이기 때문에 Electirc field는 constatnt임을 알 수 있다. 그렇기 때문에 oxide 영역세어 band bending은 선형적이고 이를 고려해서 band diagram을 그려줘야한다.
• 마지막으로, oxide와 semiconductor의 경계면을 살펴보자. 자세히 다루지는 않겠지만, 경계면에서 Gauss' Law를 적용하면 $\epsilon_{ox}E_{ox} = \epsilon_{si}E_{si}$와 같은 displacement field(변위장) 수식을 얻을 수 있다. 이를 간단히 정리하면 최종적으로 $E_{ox} \approx 3E_{si}$ 관계식을 얻을 수 있다. 이것은 semiconductor substrate와 oxide의 경계면에서 oxide의 band 기울기가 semiconductor의 bnad 기울기의 3배라는 의미이다. 이 역시 band diagram을 그릴 때 고려해주어야한다.
  $ $

위의 모든 조건을 적용하면 아래와 같은 최종 energy band diagram($\phi_m < \phi_s$인 경우의 band diagram)을 얻을 수 있다.

(참고: Semiconductor Physics and Devices (Donald A. Neamen))

그림에서도 알 수 있듯이, 고정점들을 기준으로 각각의 band를 shift하여 $E_F$는 일치시켰음을 알 수 있다.

Flat Band Voltage

Energy band diagram에서 보았듯이, MOS Capacitor에는 band bending 현상이 생긴다. 이때, $V_G$에 특정 전압을 인가하면 band bending 현상이 사라지게 되는데, 이를 flat band voltage $V_{FB}$라고 한다. $V_{FB}$는 접합 전의 $E_{FM}$과 $E_{FS}$ 차이만큼의 전압이다.

(참고: Semiconductor Physics and Devices (Donald A. Neamen))

Operation modes

위에서 Flat band voltage를 인가했을 때의 energy band diagram을 그려보았다. 그렇다면 그 이상의 전압을 인가했을 때, 혹은 그 이하의 전압을 인가했을 때는 어떤 현상이 일어나는지 알아보자.

① $V < 0$일 때(p-type semiconductor의 경우): Accumulation mode

(참고: Semiconductor Physics and Devices (Donald A. Neamen))

위의 그림을 보면 P-type semiconductor의 hole들이 metal에 인가된 (-)전압에 의해 metal 쪽으로 이동하려하지만, oxide에 의해 metal로 이동하지 못하고 경계면에 모여있는 것을 알 수 있다. 이와 같은 현상을 Accumulation(축적) mode라고 한다. 이전에 energy band diagram을 그릴 때, semiconductor 영역에서 depletion 영역이 생기는 것을 확인했는데, 그 이유가 바로 축적이다. Majority carrier인 (+) charge의 hole들이 경계면에 축적되어 depletion 영역을 형성하게 된다. 이와 같은 특징은 수식으로도 확인할 수 있다. 우리가 이미 알고있듯이 정공의 농도는 $P_0 = N_ve^{\frac{- (E_f - E_v)}{kT}}$이다. 위의 그래프를 자세히 보면 경계면에서 $E_F$와 $E_v$의 차이가 매우 작은 것을 확인할 수 있다. 즉, $E_F - E_v$가 감소하기 때문에 $P_0$는 증가하게 된다.
$ $
다시 한 번 정리하자면, $V < 0$인 경우 경계면에 majority carrier가 축적되는 현상이 발생하는데, 이것이 Accumulation mode이다.

② $V = V_{FB}$일 때(p-type semiconductor의 경우) (mode로 지칭하지 않음)

(참고: Semiconductor Physics and Devices (Donald A. Neamen))

위의 경우는 앞서 언급했던 Flat band voltage를 인가한 경우이다. 이 경우는 위에서 언급했기 때문에 그래프만 참고하고 넘어가도록 하자.

③ $V > 0$일 때(p-type semiconductor의 경우): Depletion mode

(참고: Semiconductor Physics and Devices (Donald A. Neamen))

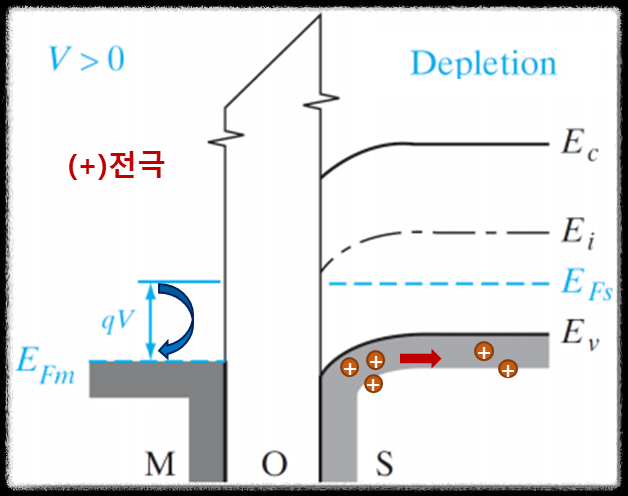
위와 같은 mode를 Depletion mode라고 한다. metal에 인가된 (+)전압에 의해 semiconductor의 (+) charge를 띄는 hole들이 경계면으로 부터 멀어져 경계면 근처에 (-) fixed charge만 남게된다. 남겨진 (-) fixed charge에 의해 depletion 영역이 형성되는 것이다.

④ $V >> 0$일 때(p-type semiconductor의 경우): Inversion mode

(참고: Semiconductor Physics and Devices (Donald A. Neamen))

위의 mode는 Inversion mode라고 하는데, 말 그대로 경계면에서의 특징이 p-type에서 n-type으로 반전된다. 인가된 전압이 매우 강하기 때문에 경계면에서 $E_{Fs}$가 $E_c$에 가까워진다. 또한, Metal에 인가된 매우 강력한 (+)전압에 의해 p-type semiconductor의 minority carrier인 전자가 경계면으로 모이게 된다. 이러한 이유로 경계면에서 n-type과 같은 특징이 나타나고 이를 p-type에서 n-type으로 반전되었다는 의미에서 inversion mode라고 한다.

 

---

작성자: 이현우 / 수정 및 검토: 손동휘, 김현수