<MS Junction> 2. 인가한 전압에 따른 특징

이번 시간에는 PN junction 떄와 마찬가지로 MS junction에 zero bias, reverse bias, forward bais를 인가했을 때 나타나는 특징과 흐르는 전류의 수식을 전개해보도록 하자.

(참고: https://youtube.com/playlist?list=PLcfIhRUEj9uAVHkFy5rbY-0pzWcZlU-0h)

들어가기에 앞서,

간단하게 forward bias를 인가했을 때, 그리고 reverse bias를 인가했을 때 전류가 어떻게 흐르는지 살펴보자.

Reverse bias, Forward bias를 인가했을 때의 전류

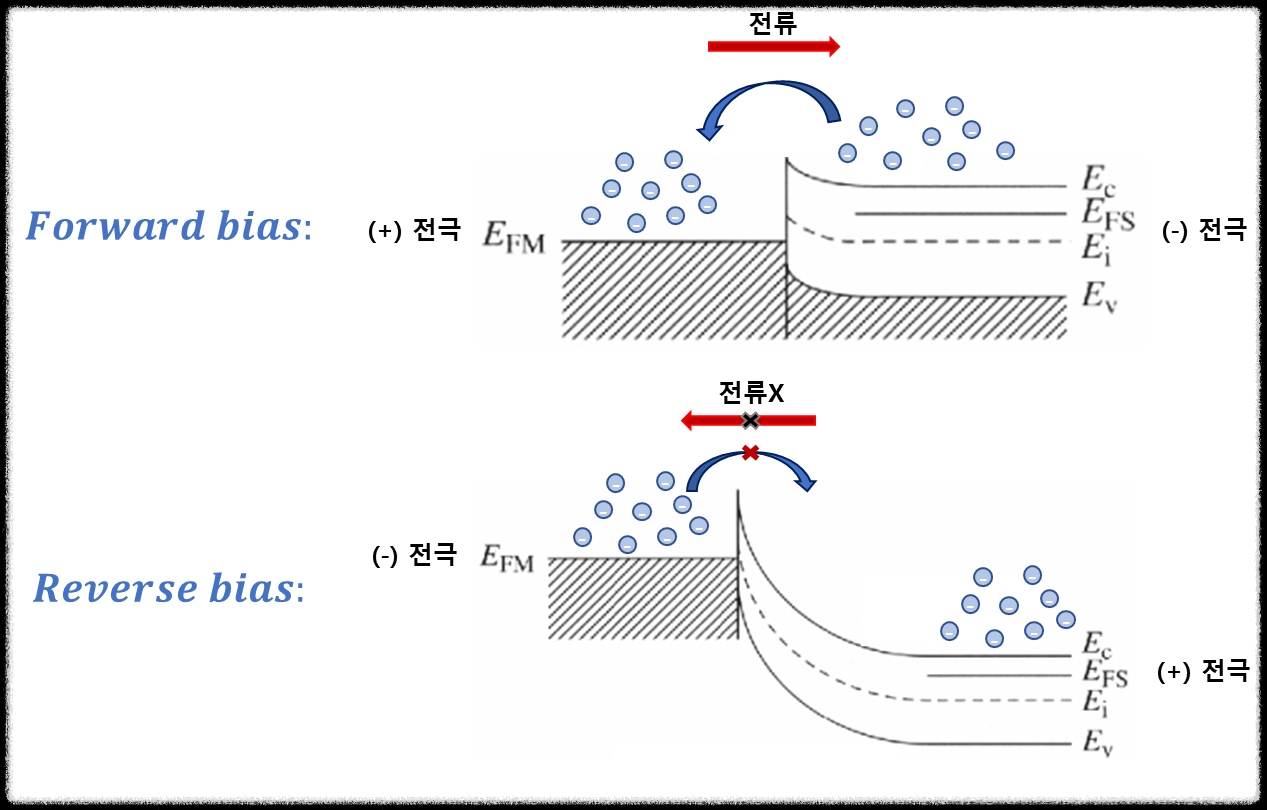
• Forward bias를 인가했을 때, 위에서 볼 수 있듯이 $V_bi$가 낮아져 majority carrier인 전자가 (-)전압이 인가된 semiconductor쪽에서 Energy barrier를 넘어 (+)전압이 인가된 metal 방향으로 이동한다. 따라서 전자의 이동방향과 반대 방향으로 전류가 흐르게 된다.
• Reverse bias를 인가했을 때, 위에서 볼 수 있듯이 $V_bi$가 매우 높아지게 된다. 이때, semiconductor에 있는 majority carrier인 전자는 (-)전압이 인가된 metal로 이동하려하지 않고, metal에 있는 전자는 (+)전압이 인가된 semiconductor로 이동하려하지만, 항상 일정한 값으로 존재하는 $\phi_{B0}$를 넘지 못해서 이동하지 못한다. 따라서 Reverse bias가 인가된 상황에서는 전류가 거의 흐르지 않는다.

$ $

참고로, 위 그림과 설명을 통해 짐작했겠지만, MS junction에서는 majority carrier에 대해 해석하면 전류에 대한 수식과 정성적인 해석을 할 수 있다. 이는 minority carrier의 해석을 통해 전류의 흐름을 해석하는 PN junction과 차이가 있다.

$ $

추가적으로, forward bias를 인가했을 때 carrier가 energy barrier를 넘어가는 현상이 있었는데, 이를 Thermionic Emission이라고 한다. 이후에 forward bias 상황에 대해 자세히 다룰 때 수식과 함께 살펴보자.

Zero bias

MS junction의 수식을 전개하기에 앞서, ohmic contact과 rectifying contact에 대한 이해가 부족하다면 앞선 챕터를 다시 한 번 공부하기를 바란다.
앞선 챕터에서 배웠듯이, ohmic contact이 이루어진 상황에서는 전류가 항상 매우 잘 흐른다. 그렇기에 우리는 ohmic contact이 아닌 rectifying contact MS junction의 수식을 전개하도록 하겠다. 수식을 전개하는 과정은 PN junction과 동일하게 아래와 같다. 계산하는 과정은 PN junction과 동일하기 때문에 계산 과정은 생략하고 결과값만 확인해보자.

Boundry conditions

위의 W값을 보면 $N_D$와 반비례 관계에 있다는 사실을 알 수 있다. 추가적으로 charge density ρ를 살펴보면 pn junction과 마찬가지로 ρ축 기준 (-) 쪽과 (+)쪽의 면적이 같아야하므로 charge density 그래프에서 semiconductor쪽의 넓이와 같은 크기의 값이 metal과 semiconductor의 경계면에 모여있다. 이는 pn junction의 one-side junction과 비슷함을 알 수 있고, 실제로 W값도 one-side junctino과 동일하다.

Reverse bias

MS junction(reverse bias)

MS junction에 reverse bias를 인가했을 때 역시 PN junction과 비슷한 결과값을 수식을 얻을 수 있다. reverse bias를 인가한 상태에서 PN junction과 마찬가지로 높아진 에너지 장벽으로 인해 전자가 이동하지 못해 전류는 흐르지 않고 전기장만 형성된... 전하가 저장된 capacitor와 같은 역할을 함을 알 수 있다. 마찬가지로 PN junction과 동일하게 depletion capacitance($C_{dep}$)를 정의할 수 있다. 실제로 $C_{dep}$ 결과값도 PN junction과 동일하게 정의됨을 알 수 있다.

$C_{dep}$

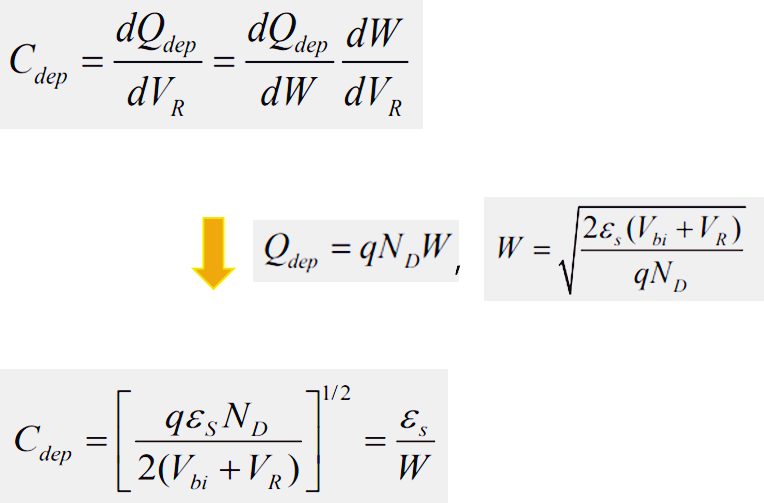
위의 식을 마찬가지로 PN junction을 해석했던 것과 같이 $V_r$과 $\frac{1}{C_{dep}^2}$의 관계식으로 표현해보자.

$V_r$과 $\frac{1}{C_{dep}^2}$ 관계식

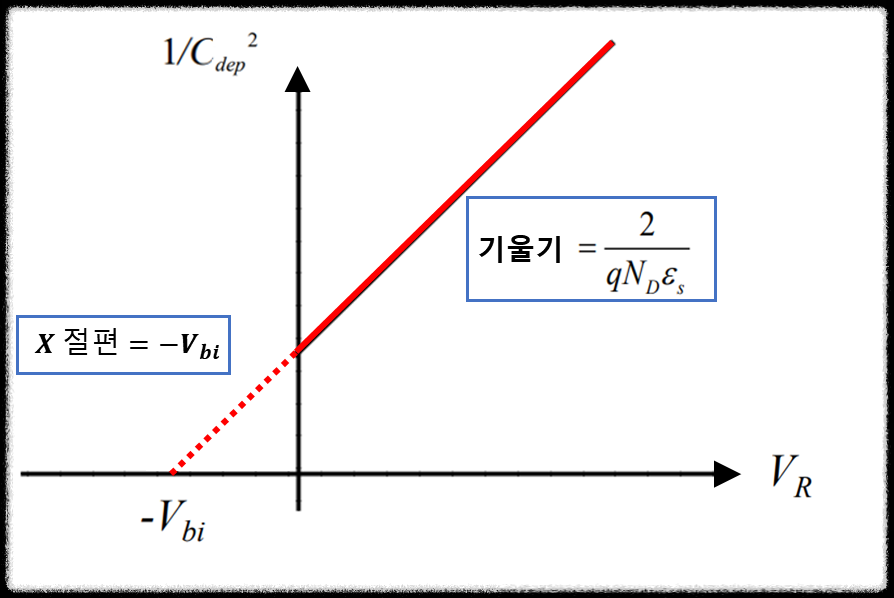
위와 같이 관계식을 형성하면, $V_R$을 바꿔가며 장비를 통해 $C_{dep}$를 측정하면 기울기와 $x$절편을 구할 수 있고, 이를 통해 $V_{bi}$와 $N_d$ 값을 도출해낼 수 있다. 여기서 한 발 더 나아가, $V_{bi}$와 $N_d$를 이용하여 아래와 같이 $\phi_{B0}$를 구할 수 있다.

$V_{bi}$와 $N_d$로부터 $\phi_{B0}$ 구하는 과정

Forward bias

이번 챕터의 제일 위에서 간단하게 살펴보았던 forward bias에서의 전류 흐름을 해석하기 위해서는 전자의 운동 에너지가 energy barrier보다 높아야 발생하는 현상인 Thermionic Emission의 수식을 이용해야한다.

Thermionic Emission

위의 수식을 전류를 구하는 수식에 대입하면 다음과 같이 표현된다.

Forward bias를 인가했을 때의 전류

위 수식을 통해, forward bais를 인가한 rectifying contect MS junction은 온($T$)도(온도에 굉장히 민감함)와 인가한 전압($V_A$)에 비례하고 schottky barrier height($\phi_{B0}$)에 반비례함을 알 수 있다.

$ $

도출한 수식을 통해, MS junction 함수를 PN junction과 비교해서 살펴보자.

MS junction, PN junction I-V 함수 /&nbsp; (참고: Semiconductor Physics and Devices (Donald A. Neamen))

위의 함수를 살펴보면 MS junction이 PN junction보다 같은 전압 대비 전류가 잘 흐른다는 것을 알 수 있다. 즉, MS junction에 더 큰 전류를 흘리는 것이 용이하다.
또다른 차이점이라면, MS junction은 semiconductor에서 majority carrier가 이동한 후에 정공과 전자가 무수히 많은 metal에서 모두 재결합되기 떄문에 PN junction과 다르게 diffusion capacitance가 발생하지 않는다.

 

---

작성자: 이현우 / 수정 및 검토: 손동휘, 김현수