<MOSFET>6. MOSFET의 비이상적인효과

이번 포스팅에서는 MOSFET의 ideal한 경우와는 다른 비이상적인효과 3가지에 대하여 알아볼 것이다. 

 

비이상적인 효과

 

1. Channel length modulation

사진 출처 :

위 그림은 MOSFET의 saturation region으로 drain쪽에 depletion region이 형성된 그림이다.

이때 $I_D$는 수평한 방향으로 흐른다.

 

채널이 끝나는 지점인 빨간 동그라미 지점에 걸리는 전압은 $V_{DS(sat)}=V_{GS}-V_T$이다. 

channel을 형성한 뒤 추가적으로 인가된 $V_{DS}$는 depletion region 양단에 인가된다.

즉 전체 $V_{DS}$는 $V_{DS}=V_{DS(sat)}+\Delta V_{DS}$이다.

 

saturation region에 들어간 MOSFET의 경우 $V_D$를 $I_D$는 일정하다.

이 같은 결과는 gate의 길이가 depletion region의 길이보다 훨씬 긴 경우에 발생한다. 

 

예를 들어

gate 길이(L)=10um >> depletion 길이($\Delta L$)=100nm인 경우에는, gate의 길이가 depletion 길이 보다 훨씬 길기 때문에 depletion의 영향이 미미하다.

하지만 L=500nm > $\Delta L$=100nm인 경우에는, 이제 더 이상 delpletion의 영향을 무시할 수 없게 된다.

이때 channel의 길이는 400nm로 depletion region이 생겨 채널의 길이가 많이 작아졌다.

 

채널의 길이가 줄어들면서 바뀌는 현상이 바로 channel length modulation이다.

이때 나타나는 현상은 무엇일까?

물리적이 해석이 들어가지 않은 수학적으로 최대한 단순화 시킨 model에 대하여 알아보자.

 

depletion region폭에 걸리는 전압은 $V_{DS(sat)}-\Delta V_{DS}$와 같다고 앞에서 언급했다.

따라서 $\Delta L$의 길이는 $V_{DS(sat)}-\Delta V_{DS}$에 비례한다고 단순히 이해해보자. 

 

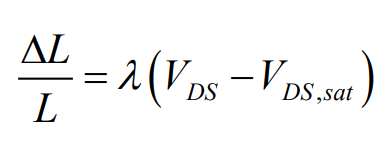
또한 위와 같이 gate length와 depletion region의 관계를 비례 상수 $\lambda$를 포함하여 정의 해보자. 

(이때  $\lambda$ 단순한 model을 만들기 위해 도입한 비례 상수이다.) 

이제 depletion region의 영향력을 전류에 포함시켜 보자.

 

위 오른쪽 식을 정리하면 

이와 같은 식을 얻을 수 있고 $\frac{\Delta L}{L}$을 위에서 구한 비례상수식을 포함한 식으로 치환하면 

$V_{DS}$에 비례하는 {$I_{D,sat}$을 얻을 수 있다.

 

사진 출처 : https://www.sciencedirect.com/topics/engineering

위 그래프는 $V_{DS}$ - {$I_{D,sat}$ 그래프이다. 

그래프를 통해 $V_{DS}$가 증가하면 {$I_{D,sat}$가 포화되지 않고 증가한다는 것을 알 수 있다.

이때 증가할 때의 기울기는 $\lambda$이다. 

 

2. Velocity Saturation(속도 포화)

이상적인 I-V모델에서 channel의 mobility는 항상 일정하다고 가정한다. 

우리는 전자의 속도가 $v=\mu E$로 mobility와 전기장에 비례한 것을 알고 있다.

하지만 전기장이 강해져 $E_{sat}$보다 커지면 커진 전계는 열을 발생시키고 이는 lattice scattering을 발생시켜 전자의 속도를 포화시킨다. 

사진 출처 :&nbsp;Semiconductor Physics and Devices (Donald A. Neamen)

 

그러면 만약 $E=\frac{V}{L}$인 전기장의 세기가 L이 짧아져서 강해지면 어떻게 될까?

사진 출처 :&nbsp;Semiconductor Physics and Devices (Donald A. Neamen)

  

 channel length가 짧아지면서 channel내부에는 강한 전기장이 형성된다.

강해진 전기장은 기존의 long channel의 보다 더 많은 열을 발생시켜 lattice scattering을 증가시킨다.

그에 따라 carrier의 velocity는 급증하지 않고 long channel보다 낮은 전기장에서 포화된다.

이는 $V_{DS}<V_{GS}-V_T$인 depletion region이 형성되지 않았음에도 drain current의 saturation을 발생시킨다. 

 

 

 

3. Mobility Variation

속도포화에서  "이상적인 I-V모델은 channel의 mobility는 항상 일정하다고 가정한다."라고 언급했었다.

그렇다면 ideal한 경우가 아닌 실제 mobility는 어떨까?

 

사진 출처 :&nbsp;Semiconductor Physics and Devices (Donald A. Neamen)

MOSFET의 channel이 형성 되어서 전자가 이동하면  $V_{DS}$와 $V_G$에 영향을 받는다.

전자는 $V_{DS}$에 의한 수평 전기장과,  $V_G$에 의한 수직 전기장에 영향을 받는데

수평 전지장에 의해 source에서 drain쪽으로 전자가 이동하고, 수직 전기장에 의해 수직운동도 동반된다. 

두 움직임이 합쳐져 대각선 움직임이 발생하며, surface쪽으로 끌려가려고 하는 성질 때문에 surface scattering을 발생시키고, 이는 기존의 수평 전기장만을 고려한 mobility보다 더 느려진다. 

 

반도체 비이상적인 효과 3가지를 알아보았다.

우리가 앞에서 알아본 I-V 모델은 이상적인 것일 뿐 실제로는 다양한 원인에 의해 값에 변화가 발생한다. 

그렇기 때문에 소자 설계시 이 부분들을 잘 고려해서 설계해야 한다. 

 

 

 

 

 

 

---

작성자: 김현수 / 수정 및 검토: 손동휘, 이현우